ExcelのSQRT関数で平方根（ルート）を計算！使い方とエラー対処法を解説

SQRT関数の基本的な使い方

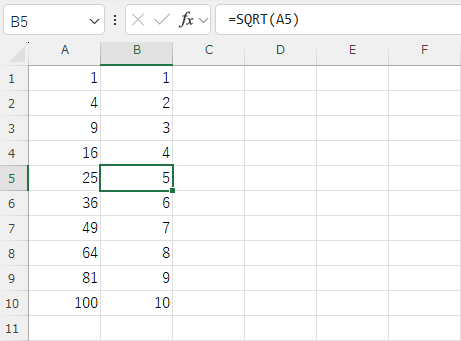
SQRT関数は、指定した数値の「正の平方根」を返します。例えば、2乗して「25」になる数は「5」と「-5」の2つがありますが、SQRT関数は必ずプラスの値である「5」を返します。

関数の構文は、引数が一つだけの非常にシンプルな形です。

=SQRT(数値)

引数には、平方根を求めたい数値、もしくはその数値が入力されているセルを指定します。

最重要ルール：引数に負の数は指定できない

SQRT関数を使う上で、絶対に覚えておかなければならないルールがあります。それは、引数にマイナスの数値を指定できないということです。もし、引数に負の数を指定した場合、Excelは計算ができないため `#NUM!` というエラーを返します。

これは、数学のルールに基づいています。「2乗してマイナスになる実数」は存在しないためです（同じ数を2回掛けても、`5×5=25`、`-5×(-5)=25` のように、結果は必ずプラスになります）。もし計算対象のデータにマイナスが含まれる可能性がある場合は、ABS関数と組み合わせる ` =SQRT(ABS(数値))` といった対策が必要になります。

もう一つの方法：「^ (1/2)」との違い

以前POWER関数の記事でも触れましたが、Excelでは「^」（キャレット）という演算子を使ってべき乗を計算できます。そして、数学の世界では「平方根を求める」ことと「1/2乗する」ことは同じ意味を持ちます。

そのため、SQRT関数を使わずに、以下のように書くことでも平方根を計算できます。

=25^(1/2)

結果はもちろん「5」となり、`=SQRT(25)` と全く同じです。

SQRT関数と「^(1/2)」、どちらを使うべき？

機能的にはどちらも同じですが、一般的には以下のような使い分けが考えられます。

• SQRT関数を使うケース：数式を見たときに、誰が見ても「平方根を求めている」という意図が明確になります。数式の可読性を重視する場合や、他の人とファイルを共有する場合には、SQRT関数が推奨されます。
• `^(1/2)`を使うケース：立方根（1/3乗）や四乗根（1/4乗）など、平方根以外の計算と合わせて使う場合に、数式の記述に一貫性を持たせることができます。

結論として、特別な理由がなければ、平方根の計算にはSQRT関数を使うのが最も分かりやすく、一般的であると言えるでしょう。

【本題】SQRT関数の実務での活用シーン

SQRT関数は、単に数値のルートを計算するだけでなく、実社会の様々な問題解決に応用されています。特に幾何学的な計算との相性は抜群です。

ケース1：幾何学での活用（三平方の定理）

学生時代に学んだ「三平方の定理（ピタゴラスの定理）」を覚えていますか？「直角三角形の斜辺の2乗は、他の2辺の2乗の和に等しい（a² + b² = c²）」という、あの有名な定理です。

この定理を応用すると、Excelを使って2点間の「直線距離」を簡単に求めることができます。例えば、ある地点から東に3km、北に4km進んだ地点があるとします。スタート地点からの直線距離は何kmになるでしょうか？これは、底辺が3km、高さが4kmの直角三角形の斜辺の長さを求めるのと同じです。

`c² = 3² + 4²` なので `c² = 9 + 16 = 25`。つまり、cの長さは25の平方根である「5km」となります。これをExcelの数式で表現してみましょう。横の距離がセルA2、縦の距離がセルB2に入力されている場合、直線距離は以下の数式で計算できます。

=SQRT(A2^2 + B2^2)

この数式は、`A2`の2乗と`B2`の2乗を足し合わせ、その合計の平方根を求めています。工場のレイアウト設計で機械間の最短距離を求めたり、マーケティング分析で顧客の店舗からの距離を算出したりと、ビジネスの現場でも非常に役立つテクニックです。

ケース2：統計学での活用（標準偏差）

データのばらつき具合を示す最も代表的な指標に「標準偏差」があります。標準偏差が大きいほどデータが散らばっており、小さいほどデータが平均値の周りに集まっていることを意味します。

この標準偏差は、「分散の正の平方根」として定義されています。Excelには標準偏差を直接計算する`STDEV.P`関数などがありますが、その関数の内部では、各データの偏差を2乗して平均した「分散」を求め、最後にSQRT関数と同じ計算で平方根を求める、という処理が行われています。統計学の世界においても、SQRT関数はデータの性質を理解するための基本的な要素として組み込まれているのです。